Realiza un gràfico de una inecuaciòn de segundo grado, explique el proceso en 5 lìneas.

Vamos a resolver la siguiente inecuación de segundo grado:

En este caso, resolver esta inecuación de segundo grado es determinar los rangos de valores de x en los que la función es mayor o igual a 0

Si al otro lado de la desigualdad no tenemos un 0, debemos pasar todos los términos al primer miembro de la desigualdad. (Esto lo explico más a fondo en el curso de inecuaciones)

Por tanto, lo primero que debemos saber qué puntos de x, hacen 0 esa función, por lo que, igual que antes, igualamos la función a 0:

Y resolvemos la ecuación de segundo grado que nos queda, obteniendo dos soluciones:

Estas dos soluciones las representamos en la recta numérica:

Nos ha quedado la recta dividida en 3 tramos. Ahora debemos saber en qué tramo la función es positiva o negativa.

Para saber si el tramo que está a la izquierda de 2 es positivo o negativo, le damos un valor a la x que esté a la izquierda de 2 en la recta, por ejemplo el 0 y vemos su resultado

Cuando x=0:

El resultado es 8, por lo que la función es positiva.

Para el tramo central, le damos un valor a la x que esté entre 2 y 4, por ejemplo el 3:

Para x=3:

El resultado es -1, por lo que la función es negativa.

Y para el tramo de la derecha le damos a la x un valor que quede a la derecha de 4. Por ejemplo el 5. Para x=5:

La función vuelve a quedar positiva.

Representamos en la recta, qué tramos son positivos y cuales negativos

Esta recta es equivalente a cuando teníamos la parábola, con el vértice apuntando hacia abajo, donde la parte que quedaba entre 2 y 4 era negativa y las otra dos partes positivas:

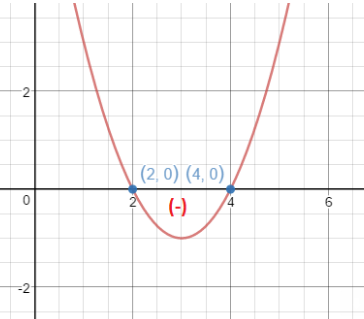
Por tanto, volviendo nuestra inecuación de segundo grado:

Esa función será positiva en los valores de x que sean menores o iguales que 2 y mayores o iguales que 4:

Por tanto, la solución será la unión de esos dos intervalos: